ゲーム木とは
ゲーム木はゲームの局面を線でつないだグラフで上から下へ伸びていく形に描いていきます。
三目並べのゲーム木
三目並べのゲーム木をPythonで描くよう、Gemini にプログラムしてもらいました。すべての枝を描くと最終局面が9!=362,880通りの結果となり描ききれなくなってしまうので、最善手のみ、しかも対称形を省略するように枝を描いてもらうようにしました。
結果はこちらです。✕初手は本来9通りありますが、対称形を省略しているので、中央・辺・隅の3通りです。✕初手隅に対して◯2手目は1通り、✕初手中央に対しても◯2手目は1通りです。それ以外は敗着になってしまうので描かれていません。最終局面は3通りに集約します。✕も◯も最善手を打つと最後は引き分けで終局します。
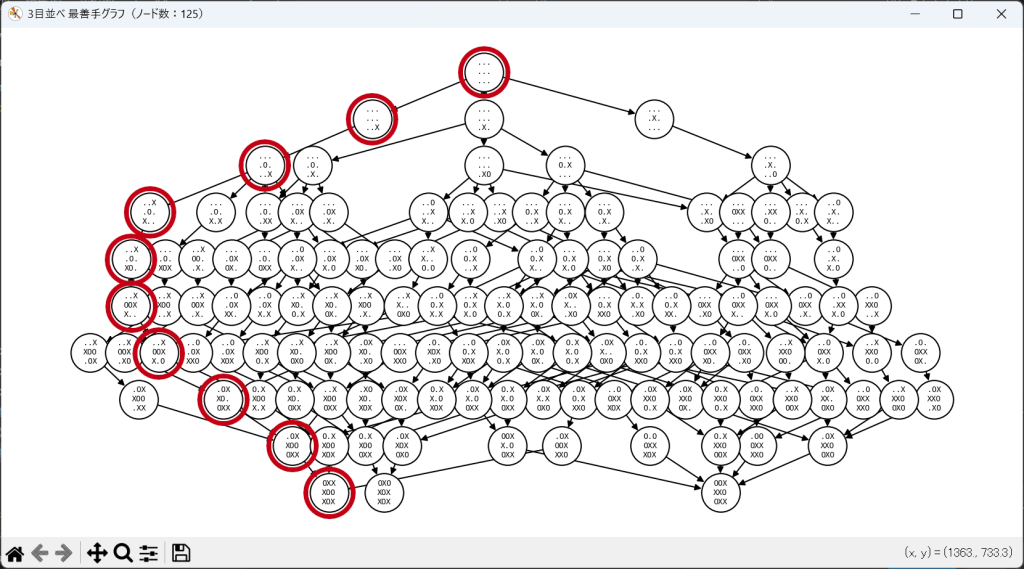
ちなみに以下のゲーム(黄色い数字は手順)の結果を上図では赤丸で示してあります。
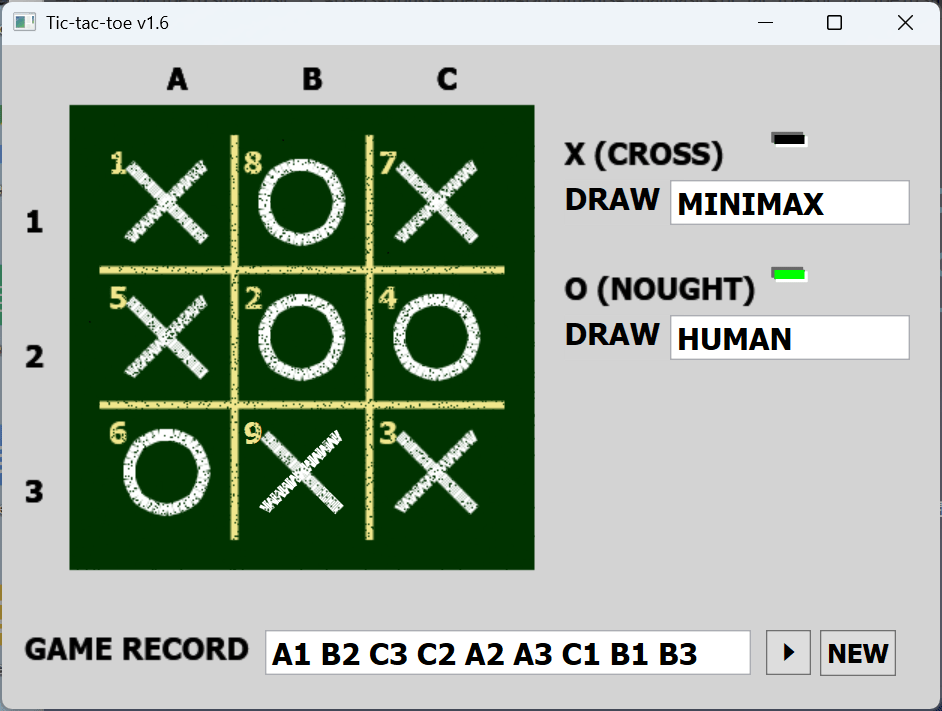
Pythonコード
ゲーム木を描くプログラムは以下の通りです。
# tic_tac_toe_tree.py
# Version: 0.1.0
# 3目並べ(Tic-Tac-Toe)の最善手を探索し、そのゲーム木を描画するプログラム
# 使用ライブラリ: networkx, matplotlib.pyplot
# Copyright © 2026 たかはしのんき. The MIT License.
import networkx as nx
import matplotlib.pyplot as plt
# --- 1. 盤面の対称性(正規化)のロジック ---
def get_canonical(board):
"""盤面の回転・反転8パターンの中で最小のものを返す"""
def rotate(b):
return (b[6], b[3], b[0], b[7], b[4], b[1], b[8], b[5], b[2])
def flip(b):
return (b[2], b[1], b[0], b[5], b[4], b[3], b[8], b[7], b[6])
states = [board]
curr = board
for _ in range(3): # 回転3回
curr = rotate(curr)
states.append(curr)
curr = flip(board)
states.append(curr)
for _ in range(3): # 反転後の回転3回
curr = rotate(curr)
states.append(curr)
return min(states)
# --- 2. ミニマックス法(評価値計算) ---
def check_win(board, player):
wins = [(0,1,2), (3,4,5), (6,7,8), (0,3,6), (1,4,7), (2,5,8), (0,4,8), (2,4,6)]
return any(all(board[i] == player for i in line) for line in wins)
memo = {}
def minimax(board, is_maximizing):
state = tuple(board)
if state in memo: return memo[state]
if check_win(board, 'X'): return 10
if check_win(board, 'O'): return -10
if '.' not in board: return 0
if is_maximizing:
best = -float('inf')
for i in [j for j, c in enumerate(board) if c == '.']:
board[i] = 'X'
best = max(best, minimax(board, False))
board[i] = '.'
else:
best = float('inf')
for i in [j for j, c in enumerate(board) if c == '.']:
board[i] = 'O'
best = min(best, minimax(board, True))
board[i] = '.'
memo[state] = best
return best
# --- 3. 最善手グラフの構築(対称性を集約) ---
def build_reduced_tree(board, player, G):
curr_canon = get_canonical(board)
if curr_canon in G: return
status = 'draw' if '.' not in board else 'in_progress'
if check_win(board, 'X'): status = 'X wins'
elif check_win(board, 'O'): status = 'O wins'
G.add_node(curr_canon, status=status)
if status != 'in_progress': return
# 現在の局面での最善のスコアを取得
is_max = (player == 'X')
best_score = minimax(list(board), is_max)
for i in [j for j, c in enumerate(board) if c == '.']:
next_board = list(board)
next_board[i] = player
# この手が最善手(スコアが一致)か確認
if minimax(next_board, not is_max) == best_score:
next_canon = get_canonical(tuple(next_board))
build_reduced_tree(tuple(next_board), 'O' if player == 'X' else 'X', G)
G.add_edge(curr_canon, next_canon)
# --- 4. 実行と描画 ---
G = nx.DiGraph()
build_reduced_tree(tuple(['.']*9), 'X', G)
# レイアウト(PyGraphvizがない場合は spring_layout を使用)
try:
pos = nx.nx_pydot.graphviz_layout(G, prog='dot')
except:
pos = nx.spring_layout(G, k=0.5)
# ラベル作成(正規化された盤面を表示)
labels = {n: f"{''.join(n[:3])}\n{''.join(n[3:6])}\n{''.join(n[6:])}" for n in G.nodes()}
plt.figure(figsize=(15, 10), num=f"3目並べ 最善手グラフ(ノード数:{len(G.nodes())})")
nx.draw(G, pos, labels=labels, with_labels=True,
node_size=900, font_size=6, font_family='monospace',
node_color='white', edgecolors='black', arrows=True)
plt.show()

